重積分する(積分領域を何とかする編)
お久しぶりです。パッパギー(@pappagie)です。
あるところで重積分の演習問題を見つけました。

初見では「ちょっと難しそうだなぁ」と思って手を付けたのですが、想像の5000兆倍骨が折れました。せっかくなのでブログの記事にしてやります。
内容のレベルは、理系の大学1年後期でやる微積と線型代数がわかっていれば読める程度にしたつもりです。
さて、この問題で一番大変そうなのは積分領域Dでしょう。

まずはここを何とかしたい。

高校数学レベルではグラフの概形すら描けません。
概形の不明な積分領域で積分しろ、と言われてもどうにもならないので、文明の利器を用いて図示してみました。

傾いた2つの楕円に挟まれた領域に見えますね。
…どうやら泥沼に足を突っ込んでしまったようです。
何がヤバいかを整理してみましょう。

ここから、大まかな方針を立ててみましょう。

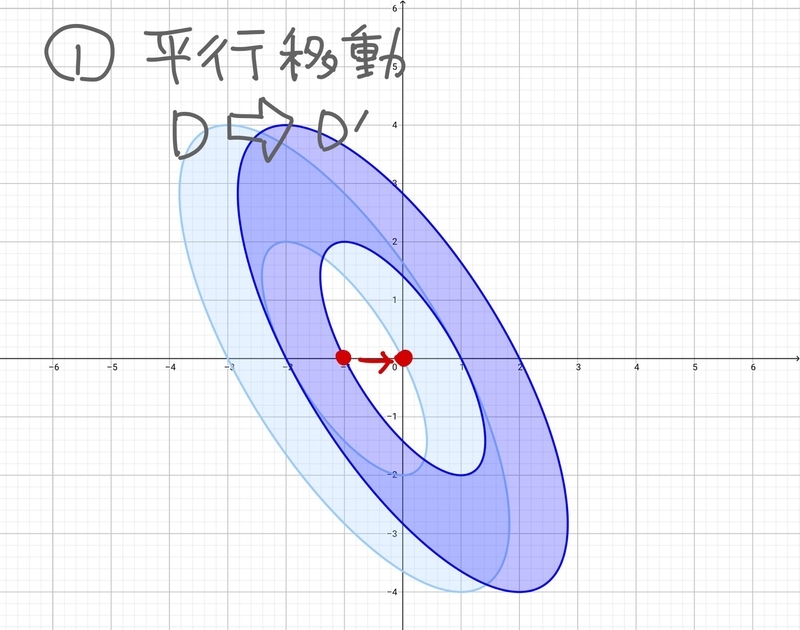
まずは①平行移動。
これはDの中心の座標が(-1,0)と分かっていたので、x軸方向に+1ずらせば座標平面の真ん中に来てくれそうです。
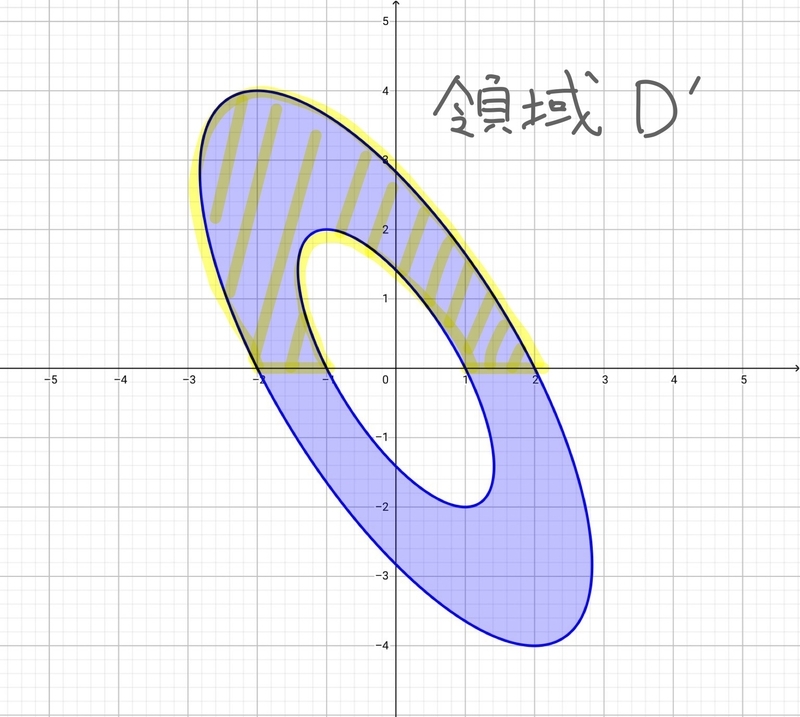
移動後の領域をD'としてあげましょう。
で、この時に式はどうなるかというと、

最初のごっつい見た目に比べると、多少シンプルになりましたね。
次は傾いているのをどうにかするために、座標軸を取り直そうと思います。
ここは線型代数のお話です。

まずは、楕円の式を行列を使って書き直します。
「そんなことできるん…?」と思うでしょう。できるんです。
工学部の線型代数の授業では、普通はやりませんが。
これを2次形式といいます。

今回はb>0なので楕円だったわけです。
で、b=0のときが特別で、いわゆる普通の楕円になるわけです。

ここまでみても( ゚д゚)となってる方が多いでしょう。
2次形式を使うと何がオイシイのかというと、真ん中の行列を対角化して座標を変換してやれば、傾いている楕円を「ただの」楕円に戻すことができることです。

実際にやってみましょう。

ここで行列の対角化が出てきます。
ここまで読んでくれた人なら誰でもできるはずです。
…が、一応丁寧に説明しておきます。
任意の数強の方は読み飛ばしてください。


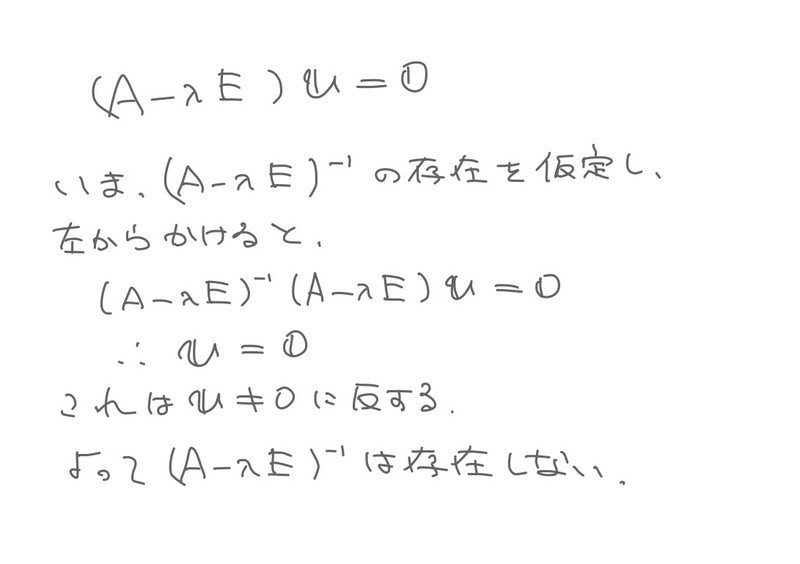
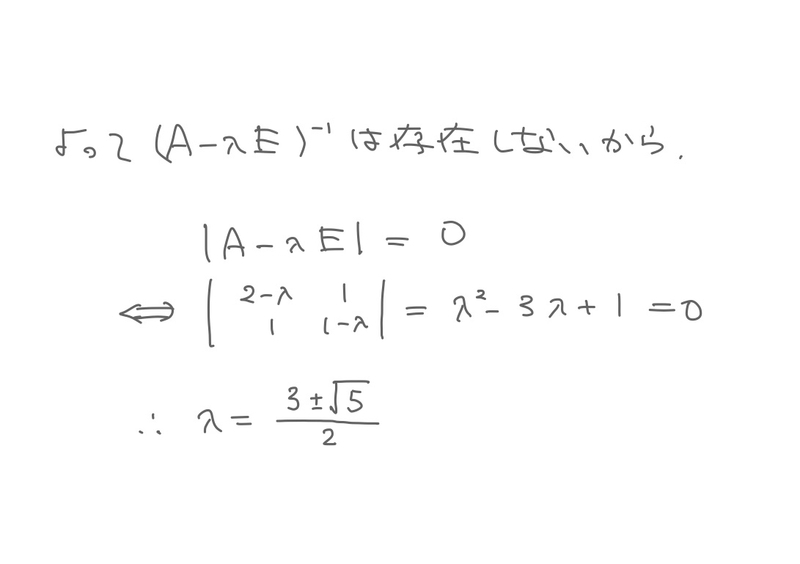


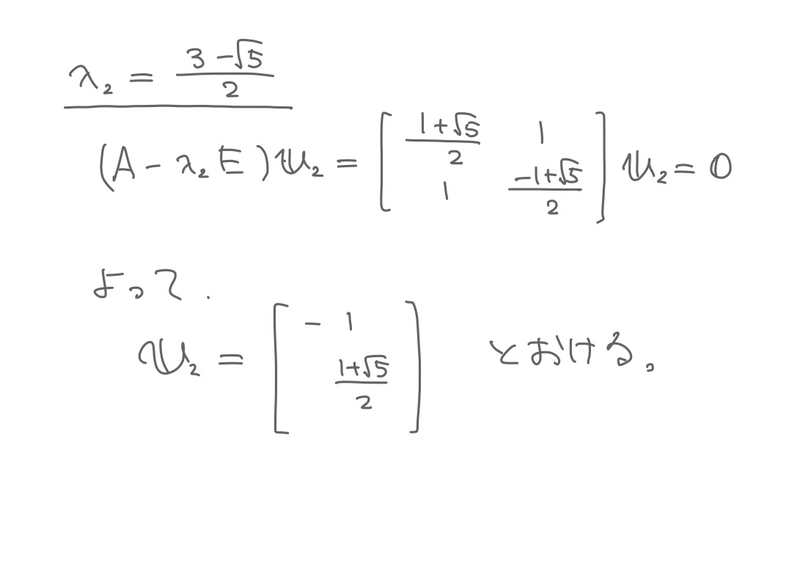
はい。ここまでは誰でもできるはずです。
この先はあまり見たことがないかもしれません。
わたしが昔読んだ『線型代数』(長谷川浩司著、日本評論社)で紹介されてたやり方です。
この方法だと、一度流れをつかんでおけば忘れにくいのでおススメしておきます。


お疲れさまでした。対角化が完了しました。
でもね、これが本題ではないのですよ。

本題は座標軸を取り直して、ただの楕円にすることでした。
対角化した行列Aを用いて、座標を取り直してみましょう。

青いところでは、行列と列ベクトルの積を新しい座標(s,t)と置きました。
赤いところでは、同じことを行ベクトルでやっただけです。
こうやって座標を取り直すと、あら不思議、ただの楕円になります。

ただの楕円の一般形だと、s^2とt^2の係数が定数の2乗の形なので、ここを何とかしたいわけです。
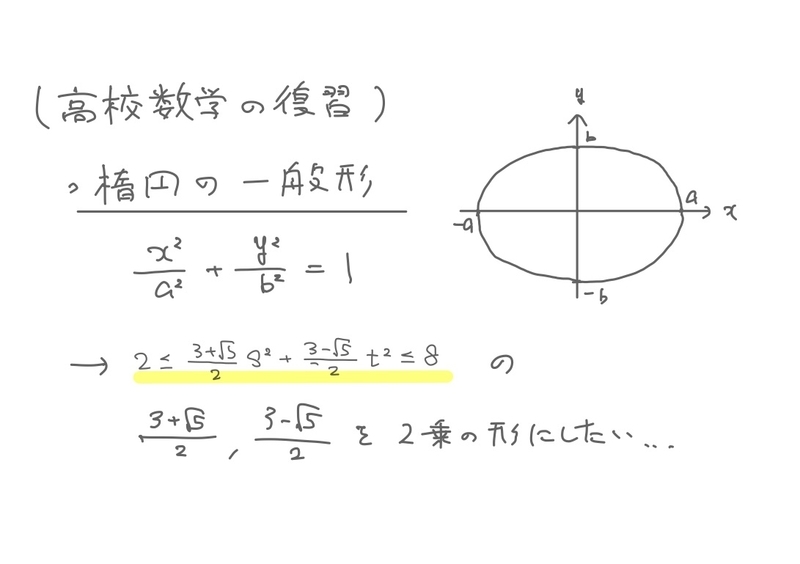
なんとかしましょう。

黄金比が出現しました。何回もルートが入った分数を書くのは面倒なので、Φでおいてあげました。1/Φの件は、もはや知らないとできませんね()
これを用いて書き換えてあげると、次のようになります。

ようやく楕円がまっすぐになってくれました。
ここで忘れていたy≧0という条件も、s,tを用いて書き換えましょう。

対角化で使った行列Pにも、実は黄金比Φが隠れていました。
適当な角度を傾けたのではなく、きっちり作問されたのだとわかります。
楕円とs+Φt≧0の領域をD"とおいて、st平面に図示すると次のようになります。

まだ終わりません。
高校数学なので特にいうことはありません。

s+Φt≧0は、前ページの(s,t)を代入して整理するとこうなります。
加法定理を使いました。
tanα=1/Φ^3は、角αとθを結ぶ重要な式です。
積分する際に使いますね。

はい。これで極座標に変換できました。
図示するとこうなります。素直な円になってくれましたね。角度が中途半端ですが。

ここまでの流れをおさらいしましょう。

中心がずれているから①平行移動し、
傾いてるのを直すために②座標軸をとり直し、
わけです。
図示するとこんな感じ。
上2つがxy平面、左下がst平面、右下が極座標であることにご注意を。

ここまで読んでくださった方、お疲れさまでした。
ところで忘れていませんか?
本問は重積分の問題だったことを…?
重積分の計算は読者の演習問題とする。(言いたかっただけ)